پلاریزاسیون، قطبش، Polarization

بسم الله الرحمن الرحیم.

مختصری راجع به موج

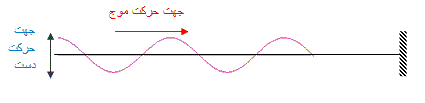
یک طناب بلند را مانند شکل زیر از یک سمت به دیوار وصل کرده و یک آشفتگی مانند شکل زیر بوسیله جابجایی دست خود در سر دیگرآن ایجاد کنید.این آشفتگی در جهت نشان داده شده شروع به حرکت خواهد کرد.

حالا اگر روند ایجاد این آشفتگی را به صورت متناوب با حرکت دست به سمت بالا و پایین ادامه دهیم مجموعه آشفتگیهایی پشت سرهم بوجود می آیند که مانند شکل زیر میتواند باشد.

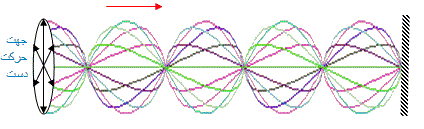
حال اگر در هر بار بالا و پایین رفتن دست جهت حرکت دست را مانند شکل عوض کنید طوری که حول یک دایره 360 درجه بچرخد شکل موجها مانند شکل زیر میشود.

موج پلاریزه

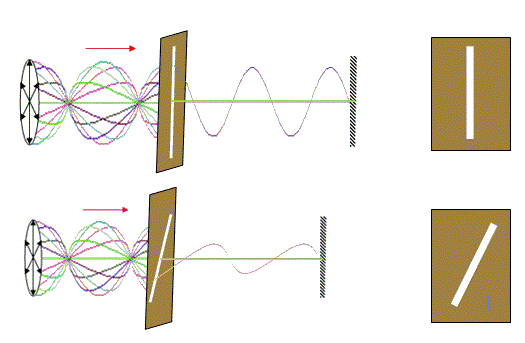
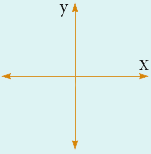
موج پلاریزه موجهایی از این دست که در همه جهتها در حال نوسان هستند موجهای غیر پلاریزه هستند.حال اگر یک فیلتر خاص سر راه این موج قرار دهیم میتوان موج خاصی را که در جهت خاص در حال نوسان است ،انتخاب نمود و به آن اجازه عبور داد مثلا در مثال طناب یک صفحه شکافدار را مانند شکل زیر بکار ببریم تنها موجهایی که در جهت شکاف هستند، قابل عبور میباشند،بنابراین موجهایی یکدست و در یک جهت نوسان خاص خواهیم داشت که به این کار پلاریزه کردن موج میگویند

پلاریزیشن ازویژگی های موج به شمار می رود و جهتگیری (orientation) نوسان های موج را مشخص می کند. این پدیده برای امواج الکترومگنتیک و امواج مکانیکی صادق است و ما به طور خاص در این جا به امواج الکترومگنتیک خواهیم پرداخت که امیدوارم مفید فایده برای علاقه مندان واقع شود. ضمنا پلاریزیشن نه فقط به عنوان پدیدارشناسی نظری که به عنوان ابزار ساز و توجیه کننده در سایر رشته های علوم و نیزدرصنعت اهمیت دارد. 

  

 

در این مقاله قصد دارم به کلیات و مقدمات موضوع قطبش (polarization) امواج بپردازم. در واقع پلاریزیشن از ویژگی های موج به شمار می رود و جهتگیری (orientation) نوسان های موج را مشخص می کند. این پدیده برای امواج الکترومگنتیک و امواج مکانیکی صادق است و ما به طور خاص در این جا به امواج الکترومگنتیک خواهیم پرداخت که امیدوارم مفید فایده برای علاقه مندان واقع شود. ضمنا پلاریزیشن نه فقط به عنوان پدیدارشناسی نظری که به عنوان ابزار ساز و توجیه کننده در سایر رشته های علوم و نیز در صنعت اهمیت دارد. از جمله کاربرد آن می توان پلاریمتری (polarimetry) مواد شیمیایی، شناسایی رفتار جانوران به ویژه نحوه جهت یابی حشرات، زمین شناسی و نجوم را نام برد. ضمنا عکاسان از کاربرد های وسیع فیلتر های پلرایزر و دیپلرایزر در عکاسی هنری و حرفه ای بهره مندند.

از سویی یکی از کاربرد های صنعتی دیگر ویژگی قطبیدگی امواج الکترومگنتیک استفاده از آن در آنتن های رادیویی و تلویزیونی و نیز در رادارها و فرستنده های ماهواره ای است. به عنوان مثال از نمود های این کاربرد این است که آتن های تلویزیونی وی اچ اف (VHF: very high frequency) در امریکای شمالی جهتگیری افقی دارند ولی در انگلستان این جهتگیری عمودی است. دلیل این امر پلاریزه خطی بودن امواج VHF فرستاده شده توسط فرستنده ها در دو راستای افقی و عمودی در امریکای شمالی و انگستان است که در ادامه متوجه مفهوم آن خواهیم شد.

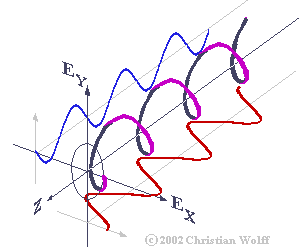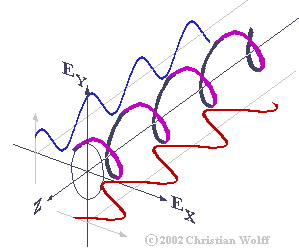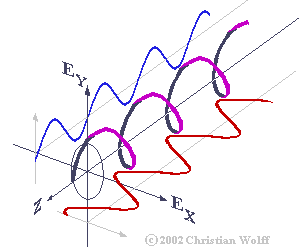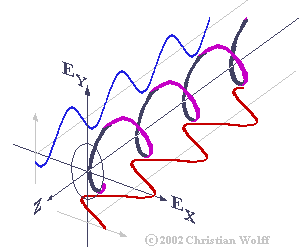
اما پیش از آن که به بررسی ریاضی پلاریزیشن برسیم باید مفاهیم هندسی آن را دریابیم. می دانیم هنگامی که یک چشمه موج نقطه ای (مثلا فقط یک تک الکترون اتم هیدروژن برانگیخته) موج الکترومگنتیک گسیل کند شکل موج آن به صورت زیر خواهد بود.

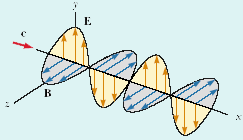
اگر هر یک از میدان های الکتریکی یا مغناطیسی را در نظر بگیریم می توانیم یک صفحه گذرا بر میدان رسم کنیم. که به آن صفحه نوسان (oscillating plane) می گویند. حال اگر از جلو به این صفحه نگاه کنیم ان را به صورت خطی که حرکت نوسان ساده (SHM) دارد خواهیم دید. و اگر کل مسیر نوسانش را رسم کنیم چیزی مشابه شکل زیر خواهد شد.

و این دقیقا حالت پلاریزیشن خطی است! همان طور که در تعریف پلاریزیشن آوردیم، این خط نشان می دهد که میدان الکتریکی موج ما چگونه جهت گیری کرده است. (و همین طور میدان مغناطیسی که عمود و مرتبط با آن است.) حال تصور کنید که n الکترون که به حالت پایه بازمی گردند و موج گسیل می کنند، اگر همه جهت گیری میدان الکتریکی (یا مغناطیسی) شان موازی با صفحه ای باشد که رسم کردیم، می گوییم نور پلاریزه خطی است(linear polarized) . قطبیدگی نور مانند ویژگی های نور لیزر است. همان طور که برای لیزر می گوییم تمام فوتون ها هم فاز، هم بسامد و هم دامنه هستند، این جا می گوییم همه فوتون ها جهتگیری الکتریکی (یا مغناطیسی) مشابه دارند.

ضمنا همانطور که ما منبع طبیعی نور لیزر نداریم چرا که هیچ منبعی تمام فوتون ها را در یک بسامد و با زاویه فاز یکسان تولید نمی کند، هیچ منبع نوری نیز نور طبیعی پلاریزه تولید نمی کند. تصور بفرمایید که یک چشمه شامل تعداد n ذره گسیلنده موج می باشد. هر یک از فوتون های گسیل شده در این حالت می توانند جهت گیری رندم میدان الکتریکی داشته باشند. و به طور آماری می توان تصور کرد برای تعداد زیاد ذرات، جهت گیری میدان الکتریکی در غیاب میادین خارجی در تمامی راستا ها یکسان توزیع شده است.( به عبارت دیگر یک درجه آزادی (degree of freedom) برای میدان ایجاد شده است.) به طوری که اگر صفحات گذرنده از همه میدان ها را رسم کرده و بار دیگر از جلو به همه آن ها نگاه کنیم چیزی شبیه شکل زیر را خواهیم دید:

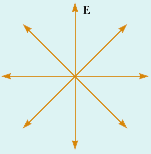
و این شکل در حقیقت همان طور که گفته شد متعلق به نور طبیعی غیر پلاریزه (unpolarized light) می باشد. اما ما برای بسیاری از کاربرد ها از قبیل همان آنتن های رادیو تلویزیونی که ذکر شد، نیاز داریم تا موج پلاریزه معینی گسیل کنیم. برای پلاریزه کردن امواج در بسامد های گوناگون از روش های مختلفی استفاده می شود که در این جا مورد بحث ما نیست ولی به روش های ساده پلاریزیشن نور معمولی که از آن در فیلتر های پلارایزر عکاسی و یا عینک های آفتابی پلارایزر استفاده می شود می پردازیم. اگر به گرافی که  بالا رسم کردیم دقت بفرمایید، واضح است که می توانیم آن را به راحتی به دو مولفه متعامد تجزیه کنیم. و به این ترتیب در واقع نور غیر پلاریزه را به دو دسته پرتو پلازیره متعامد تجزیه کرده ایم.

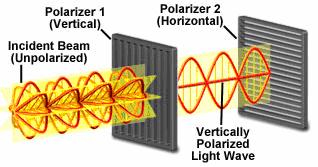
اگر ما بخواهیم در هر یک از دو راستا به نور کاملا پلاریزه دست یابیم باید پرتو های با پلاریزیشن مخالف (عمود بر محور پلاریزیشن) را حذف کنیم. که برای این منظور ساده ترین روش استفاده از صفحه قطبنده (polarizing sheet) است که اولین بار در 1932 توسط ادوین لند (Edwin Land) ساخته شد. وی در دوران دانشجویی اش مولکول بلند خاصی را یافت و آن را بر روی پلاستیک چسباند. سپس با کشیدن پلاستیک، مولکول های ماده را روی پلاستیک به شکل یک توری در آورد. چیزی که امروز از آن با نام پلاروئید (Polaroid) یاد می شود و اساس ساز و کار عینک های آفتابی و فیلتر های عکاسی پلارایزر را تشکیل می دهد. که شماتیک آن مانند تصویر زیر است.

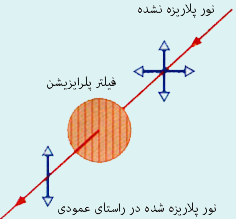
حال می توانیم شدت این نور را نیز بررسی کنیم. اگر شدت نور ورودی به فیلتر را I₀ بنامیم، با توجه به این که گفتیم جهتگیری میدان الکتریکی یک درجه آزادی دارد، نتیجه مستقیم آماری آن است که جهت گیری ها به طور یکنواخت در تمام راستاها توزیع شده است و بنا براین پس از تجزیه به مولفه های افقی و عمودی، نیمی از نور جهت گیری افقی و نیم دیگر جهت گیری عمودی خواهد داشت. پس بعد از عبور از فیلتر پلرایزر عمودی به شکل بالا، تمام مولفه های افقی نور جذب خواهند شد و در نتیجه شدت نور دقیقا نصف خواهد شد. یعنی I=I₀/2. حالا آن چه ما داریم یک نور پلاریزه عمودی است. اما ما می توانیم دوباره آن را در جهت دیگری پلاریزه کنیم. این بار محور پلاریزیشن را مورب و با زاوایه θ نسبت به محور قبلی (عمودی) انتخاب می کنیم. در این حالت دستگاه کارتزین جدید را بر پایه محور مورب جدید می نویسیم و واضح است بار دیگر می توانیم پرتوهای عمودی قبلی را بر پایه دستگاه مورب به مختصات دوگانه دیگری تجزیه کنیم.

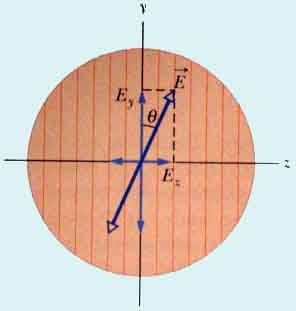
در این حالت خواهیم داشت:

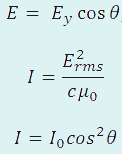
بنابراین در حالت کلی تر چیزی مثل شکل زیر داریم که نور را در هر راستایی پلاریزه می کند. (به فیلتر دوم همان طور که در شکل هم آمده آنالایزر نیز گفته می شود.

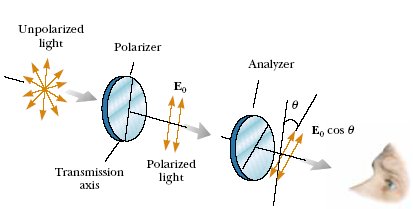
هم از رابطه و هم از شکل بالا می توان دریافت که اگر دو فیلتر پلارایزر مشابه را با زاویه 90 درجه نسبت به هم قرار دهیم شدت نور عبوری از آن ها صفر خواهد شد (cos 90=0). و این چیزی است که در شکل زیر توسط دو عینک پلارایزر مشاهده می شود.

حالا که این ویژگی موج را به صورت تجربی و هندسی فرا گرفتیم، می توانیم به بررسی ریاضی پلاریزشن بپردازیم. البته بررسی دقیق و کامل این پدیده پیچیده خواهد بود و ما از آن امتناع می کنیم و تنها به بررسی نحوه ایجاد پلاریزیشن و انواع آن خواهیم پرداخت. برای این کار نگاه خود را معطوف امواج مسطح الکترومگنتیک می کنیم. که تقریب بسیار خوبی برای این موج در فواصل دور از منبع است. در این حالت معادلات مکسول به طور خاص به معادله گاوس کاهش پیدا کرده و حاصل آن تعامد دو میدان الکتریکی و مغناطیسی است. و چنان که تا اینجا نیز دیدیم، مرسوم آن است که فقط از میدان الکتریکی کمک می گیریم و معادلاتمان را بر پایه آن می نویسیم. بنابراین فقط با یک میدان برداری دو بعدی سر و کار داریم که می توانیم این میدان را دستگاه منختصات کارتزین به طور دلخواه به دو مولفه x و y تجزیه کنیم و داریم:

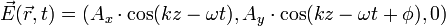
که در آن A_x و Ay هر کدام دامنه موج در راستای x و y انتخابی ماست و z نیز راستای انتشار موج خواهد بود. بنابراین اگر گراف این میدان برداری را رسم کنیم مانند شکلی که در زیر آمده است، بر روی دو صفحه x و y دو نمودار سینوسی خواهیم داشت که الزاما از نظر بسامد با هم برابرند ولی دامنه و زاویه فاز اولیه آن ها می تواند تغییر کند و بستگی به دستگاه مرجع ما نیز دارد. و در واقع همین تغییرات است که نوع پلاریزیشن را تعیین می کند. به  طور کلی انوع مختلفی از پلاریزشین وابسته با ضابطه میدان برداری الکتریکی  داریم که ما در اینجا به سه نوع خطی، دایره ای و بیضوی می پردازیم و البته می دانیم که با دانش هندسه تحلیلی می توانیم هر سه تای آن ها را با معادله پارامتری بیضی مشخص کنیم و عامل تعیین کننده نیز مقدار خروج از مرکز (eccentricity) بیضی خواهد بود. نمودار های زیر مربوط به حالت های پلاریزشین معروف به Lissajous figure می باشند.

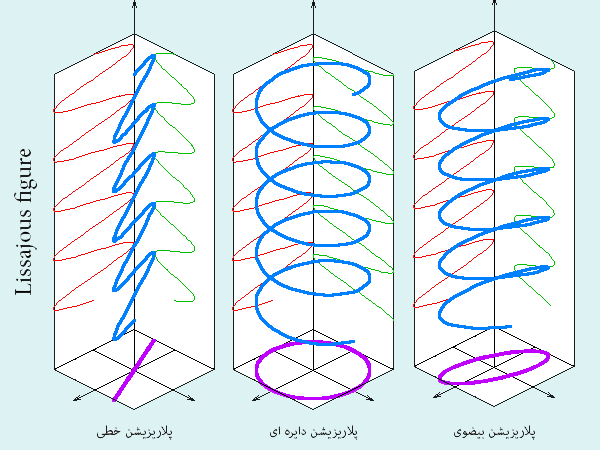
در این گراف ها، نمودار آبی مربوط به میدان برداری الکتریکی بوده و نمودارهای سبز و قرمز تجزیه مولفه های میدان برداری الکتریکی را روی صفحات نشان می دهند. و آن چه با رنگ بنفش نشان داده شده است تصویر میدان برداری بر صفحه عمود بر راستای حرکت است که پیش تر نیز از آن بحث کردیم.

حال به نمودار سمت چپ نگاه کنید، دو مولفه بردار هم دامنه، هم بسامد و هم فاز می باشند، در نتیجه پلاریزیشن خطی می باشد، در نمودار وسط دو مولفه بردار هم بسامد و هم دامنه هستند ولی نسبت به هم دقیقا در فاز مقابلند (اختلاف فاز 90 درجه) که حاصل آن پلاریزیشن دایره ای است و در نمودار سوم مولفه های بردار هم بسامد بوده ولی از نظر دامنه و فاز مقادیر دلخواه نابرابر اختیار کرده اند که سرانجامش پلاریزیشن بیضوی بوده است. می توانیم تصویر میدان برداری الکتریکی را به تنهایی مورد بررسی قرار دهیم که در حالت کلی شکل زیر را برای میدان برداری با ضابطه ای که تعریف کردیم روی صفحه عمود بر راستای انتشار خواهیم داشت:

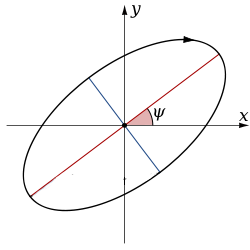
اگر این جا نسبت قطر کوچک به قطر بزرگ بیضی را منظور کنیم به کمیتی به نام ellipticity خواهیم رسید. که اگر مقدار آن 0 باشد، پلاریزیشن خطی است، اگر 1 باشد، دایره ای است و اگر مقداری بین 0 و 1 باشد، بیضوی خواهد بود. ضمنا در محاسبات آرکتانژات زاویه میان محور افقی و قطر بزرگ بیضی نیز مورد استفاده است که البته ادامه مباحث ریاضی خارج از حوصله این بحث است ولی برای مطالعه بیش تر باید دانست که این مطالعات بر پایه بردار های مختلط جونز (Jones complex vectors) و ماتریس های مختلط صورت می گیرد که می توان از آن ها بهره گرفت.

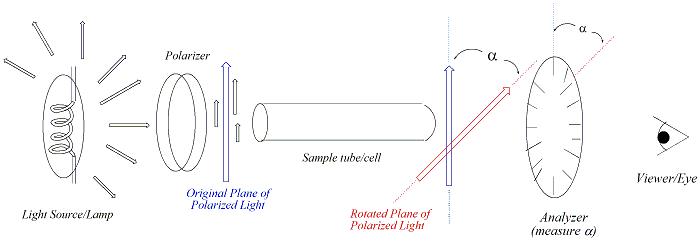
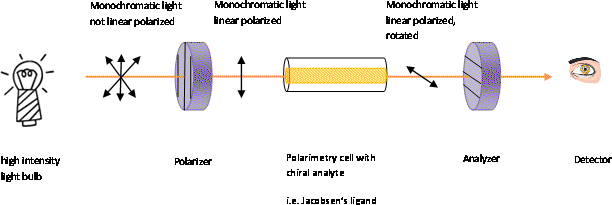
طرز کار پولاریمتر

در پولاریمتر ، پولاریزور و آنالیزور هر دو از نوع منشور نیکول انتخاب می‌شوند و بین این دو لوله آزمون قرار می‌گیرد که مختص محلول مورد آزمایش است. استفاده از منشور نیکول برای ایجاد نور قطبیده و تعیین میزان چرخش نور است. اساسا می‌توان دو منشور را عمود بر هم قرار داد که بدین ترتیب  شدت نور در عدم حضور نمونه به کمترین مقدار خود می‌رسد. نمونه با چرخش نور ، شدت نور را افزایش می‌دهد و با چرخش آنالیزور می‌توان دوباره نور را به حداقل رساند. مقدار زاویه چرخش آنالیزور مربوط به قدرت چرخش نمونه است.

از آنجا که نمی‌توان کمترین مقدار شدت نور را با چشم و یا ردیابهای فتوالکتریک تعیین کرد، لذا از دستگاهی به نام سایه ساز استفاده می‌شود. این دستگاه یک تیغه نیم موج است که بین لوله و پولاریزور قرار می‌گیرد و به کمک آن دو نیم دایره که یکی روشنتر از دیگری است ایجاد می‌شود، قسمت روشن مربوط به نیمی از نور است که از تیغه عبور می‌کند و نیمه تاریک مربوط به نیم دیگر نور است که از اطراف تیغه می‌گذرد. 
با چرخش آنالیزور هر دو نیم دایره از نظر شدت نور برابر می‌شوند.

در عدم حضور نمونه ، درجه‌ای که روشنایی دو نیم دایره یکسان شد، صفر دستگاه می‌باشد. 
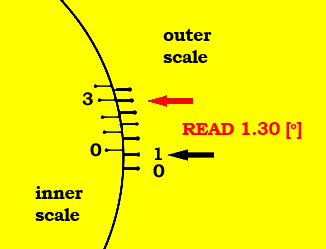
اگر نمونه از نظر نوری فعال باشد، با قرار دادن آن در لوله ، دوباره دو نیم دایره تاریک و روشن دیده می‌شود. سپس با چرخش آنالیزور شدت نور یکسان می‌شود و درجات چرخش از روی صفحات مندرج آنالیزور خوانده می‌شود. با استفاده از دستگاههای فتوالکتریک بجای چشم می‌توان میزان چرخش را با دقت 0.001 درجه تعیین کرد. 

تصاویر زیر نیز به درک بهتر موضوع کمک می کنند:

Most physical properties of enantiomers i.e., melting point, boiling point, refractive index, etc. are identical. However, they differ in a property called optical activity, in which a sample rotates the plane of polarization of a polarized light beam passing through. This effect was first discovered in 1808 by E.L. Malus, who passed light through reflective glass surfaces. Four years later, J.B. Biot found that the extent of rotation of the light depends on the thickness of the quartz plates that he used. He also discovered that other compounds i.e., sucrose solutions were capable to rotate the light. He attributed this "optical activity" to the certain features in their molecular structure (asymmetry). Because of his research, he designed one of the first polariscopes, and formulated the basic quantitative laws of polarimetry. In 1850, Wilhelmy used polarimetry to study the reaction rate of the hydrolysis of sucrose. In 1874, van't Hoff proposed that a tetrahedral environment of the carbon atom could explain the phenomenon of optical activity. Today, polarimetry is used routinely in quality and process control in the pharmaceutical industry, flavor, fragrance and essential oil industry, food industry, and chemical industry. The optical purity of the product can be determined by measuring the specific rotation of compounds like amino acids, antibiotics, steroids, vitamins, lemon oil, various sugars, and polymers and comparing them with the reference value (if the specific rotation of the pure enantiomer is known).

How does it work? Normal monochromatic light contains light that possesses oscillations of the electrical field in all possible planes perpendicular to the direction of propagation. When light is passed through a polarizer (i.e., Nicol prism, Polaroid film) only light oscillating in one plane will leave the polarizer ("picket fence model"). This linear polarized light can be described as a superposition of two counter-rotating components, which propagate with different velocities in an optical active medium. If one component interacts stronger than the other with a chiral molecule, it will slow down and therefore arrive later at the observer. The result is that the plane of the light appears to be rotated.

In a polarimeter (figure 2), plane-polarized light is introduced to a tube (typically 10 cm in length, figure 3) containing a solution with the substance to be measured. If the substance is optical inactive, the plane of the polarized light will not change in orientation and the observer will read an angle of [a]= 0^o. If the compound in the polarimetry cell was optical active, the plane of the light would be rotated on its way through the tube. The observed rotation is a result of the different components of the plane polarized light interacting differently with the chiral center. In order to observe the maximum brightness, the observer (person or instrument) will have to rotate the axis of the analyzer back, either clockwise or counterclockwise direction depending on the nature of the compound. For clockwise direction, the rotation (in degrees) is defined as positive ("+") and called dextrorotatory (from the Latin: dexter=right). In contrast, the counterclockwise direction is defined as negative ("-") and called levorotatory (from the Latin laevus=left). Unfortunately, there is no direct correlation between the configuration [(D/L) in Rosanoff, (R/S) in Cahn-Ingold-Prelog nomenclature] of an enantiomer and the direction [(+) or (-)] in which they rotate plane-polarized light. This means that the R-enantiomer can exhibit a positive or negative value for the optical rotation depending on the compound. In some cases, the solvent has an impact on the magnitude and the sign as well i.e.,(S)-lactic acid exhibits an optical rotation of [a]= +3.9^o in water and [a]= +13.7^o using 2 M sodium hydroxide solution as solvent because the observer looks at a different species (lactate).

The specific rotation [a] depends on the length of the tube, the wavelength that it is used for the acquisition, the concentration of the optical active compound (enantiomer), and to a certain degree on the temperature as well. However, the temperature effect is very difficult to specify since it differs for each compound. For instance, the [a]-value for a-pinene only slightly increases in the range from 0 ^oC to 100 ^oC (at l=589.3 nm), while it is almost cut in half for b-pinene. These two compounds only differ by the position of the alkene function.

Generally the following equation is used to calculate the specific optical rotation from experimental data:

a = observed optical rotation

c = the concentration of the solution in grams per milliliter

l = the length of the tube in decimeters (1 dm=10 cm)

Example 1:

A student obtained the following specific optical rotation from his measurement. 

This notation means that the measurement was conducted at 25 ^oC using the D-line of the sodium lamp (=589.3 nm). A sample containing 1.00 g/mL of the compound in a 1 dm tube exhibits an optical rotation of 3.5^o in clockwise direction. Note that the instrument used in Chem 30CL can provide the specific optical rotation , which already corrects the optical rotation for the cell dimensions and the concentration. The optical rotation is raw data, which does not include these corrections. It is very important to pay attention which mode was used to acquire the data! 

As mentioned earlier, polarimetry can be used to determine optical purity of enantiomers. 

Example 2: 

The observed specific optical rotation of a compound is [a]= +7.00^o. The specific optical rotation for the pure enantiomer is . 

Percent optical purity

The sample consists of 75% of the racemic form (=equimolar mixture of both enantiomers, a=0^o) and an excess of 25% of the enantiomer in question (62.5 % and 37.5 %).

The instrument used below allows you to calculate the specific rotation, if you know the concentration of the solution. The cell used for the measurement has a pathlength of 10.0 cm.

Actual polarimeter used in the lab (Autopol IV) located in YH 6104

Polarimetry cell (5 cm stainless steel cell shown here)

Practical Aspects

The cell has to be handled carefully since it costs more than $1000 to manufacture. It has to be cleaned thoroughly after the measurement was performed and is returned to the teaching assistant or instructor. Special attention should be given to the inlets that have been broken off several times already due to negligence on the student’s part!

1. The instrument has to warm up for at least 10-15 minutes, if it is not already turned on. The switch is located in the back of the instrument. The proper wavelength is chosen.

2. A solution with a known concentration (~0.5-3 %) of the compound in the proper solvent is prepared.

3. The polarimetry cell is filled with the solvent. After filling the cell, the path through the cell should be clear (If the path is not clear, the air bubbles in the path have to be removed prior to the measurement). The cell is placed on the rails inside the instrument, all the way on either the right or the left side. 

4. The "Zero button" is pressed to zero the instrument. The screen should show 0.000 and not fluctuate too much. If this is not the case, make sure that the light can pass through. If this does not solve the problem, inform the teaching assistant or instructor about this problem immediately.

5. Then, the solvent is removed and the cell is dried. The solution of the compound is filled into the dry polarimeter cell making sure that the entire inner part is filled without any air bubbles or particulate matter. 

6. The "I" button on the keypad is pressed and specific rotation is selected.

7. The proper cell dimension is selected: 100 mm (the cell provided is 100.0 mm=1 dm long)

8. Next, the proper concentration in % is entered (=the actual concentration of your solution and not the one recommended since they will most likely differ slightly!)

9. The reading on the display (=specific optical rotation) is recorded including the sign. (The experimenter has to research the literature data before performing the measurement in order to see if he is in the correct ballpark!).

10. The cell is taken out, cleaned thoroughly with the solvent used for the measurement and returned it to your teaching assistant or instructor. If the student is the last one to perform a measurement for the day, the instrument has to be turned off as well.

11. The sample from the optical rotation measurement can be recovered after the measurement if needed by removing the solvent i.e., Jacobsen ligand.

12. It is entirely unacceptable that the student locks up the cells somewhere, where they are not available to others because all the students in the course use the polarimetry cells. Doing so will result is a significant penalty for the student at fault

Specific rotation α is mearured in degrees:

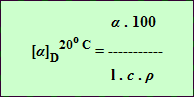(1)

D - wave lenght of sodium-spectrum (589 nm)
α - optical rotation in degrees
l - path lenght in decimetres (in our case = 1)
c - concentration of agent in 100 g of solution
ρ - density of solution

MEANING OF POLARIMENTRY

Polarimetry is used for qualitative or quantitative evaluation of optically active agents in research as well as in practice, e.g. in the sugar industry to measure syrup concentration, in chemistry to characterize substances in solution, in optical mineralogy to help to identify certain minerals in thin sections, in medicine for mesurement of sugar in urine or blood, proteins, steroids, vitamines, or alkaloids.

AIM of the task: To get principal experience with the polarimetic measurements and to identify concentrations of unknown samples of sucrose.

Classic polarimeter

Polarimeter OPTECH PL1

MEASUREMENTS WITH OPTECH PL1

Fill the polarimetric tube with tested solution, close it, dry the closing glasses, and put the polarimetric tube into the body tube; Turn the driver to the left, and find picture of the 1st stopping (see figure); Then turn the driver to the right, and find picture of the 2nd stopping; Afterwards turn the driver a little back until you find the picture filled with neutral grey, then read the result;     1st stopping     neutral grey 2nd stopping    Read resulting value: Read on the right-hand scale. It consists of the inner and outer scales: "0" point of the inner scale points units on the outer scale; the bar of the inner scale that is just opposite to a bar on the outer scale points decimal places (value read on the inner scale). On the following figure the measured value is 1.30o (always read on 2 decimal places).

PROCEDURE

Solutions: From the stock solution of 50% sucrose prepare the following solutions: 2.5; 5.0; 10.0; 15.0, and 20.0%, 50 ml each; for the calculation use theRULE OF THREE:  RULE OF THREE E.g.: to prepare 2.5% solution from the stock solution (50%): 50% .............................. 50 ml 2.5% ............................. x ml consequently: (50 x 2.5) / 50 = 2.5 ml. To prepare 2.5% solution use 2.5 ml of the stock solution (50%) and supplement it up to 50 ml with deionized water. Measurements: Measure all solutions of sucrose plus 3 unknown samples (I, II, and III), 5times each. Calculate the average value for each series of measurements; Results:

References:

1. Halliday /Resnik /Walker, Fundamentals of physics, 7^th Ed., John Wiley & Sons.

2. Halliday /Resnik /Walker, Fundamentals of physics, electronic version (pictures adopted from here.)

3. Wikipedia, the free encyclopedia, under title: “Polarization”.

4. Boston University, Department of Physics, lectures on “polarization and scattering”

5. Colorado university, department of physics, physics2000 project website: (some pictures adopted)

http://www.colorado.edu/physics/2000/polarization/index.html

6. Hyper Physics website:  under title “Polarization concepts.”

http://hosein-shimi.blogfa.com/